Control Variates for Simulation
These papers concern analysis of design of simulation algorithms based on the control variate method, with application to control and performance evaluation in network models.
Performance evaluation and policy selection in multiclass networks
S. G. Henderson, S. P. Meyn, and V. Tadic
Abstract: This paper concerns modelling and policy synthesis for regulation of multiclass queueing networks.
A 2-parameter network model is introduced to allow independent modelling of variability and mean processing-rates, while maintaining simplicity of the model. Policy synthesis is based on consideration of more tractable workload models, and then translating a policy from this abstraction to the discrete
network of interest.
Translation is made possible through the use of safety-stocks that maintain feasibility of workload trajectories.
This is a well-known approach in the queueing theory literature, and may be viewed as a generic approach to avoid deadlock in a discrete-event dynamical system.
Simulation is used to evaluate a given policy, and to tune safety-stock levels. These simulations are accelerated through a variance reduction technique that incorporates stochastic approximation to tune the variance reduction. The search for appropriate safety-stock levels is coordinated through a cutting plane algorithm.
Both the policy synthesis and the simulation acceleration rely heavily on the development of approximations to the value function through fluid model considerations.
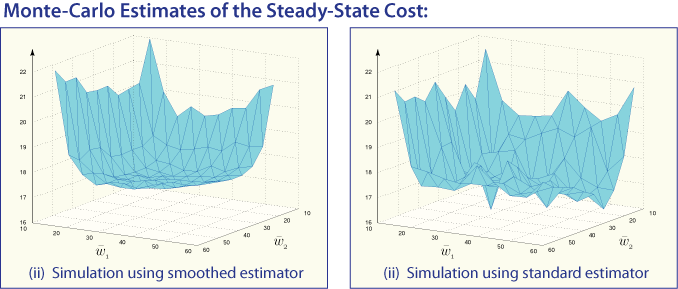 |
Numerical results for a stochastic network: Estimates of the steady state customer population in the KSRS model as a function of 100 different safety-stock levels. Two simulation experiments are shown, where in each case the simulation runlength consisted of 200,000 steps. The left hand side shows the results obtained using the smoothed estimator; the right hand side shows results with the standard estimator | |
@article{henmeytad03a,
Author = {Henderson, S. G. and Meyn, S. P. and Tadi{\'c}, V. B.},
Journal = DEDS,
Number = {1-2},
Pages = {149--189},
Title = {Performance evaluation and policy selection in multiclass networks},
Volume = {13},
Year = {2003}}
Computable exponential bounds for screened estimation and simulation
I. Kontoyiannis and S. P. Meyn
Suppose the expectation E(F(X)) is to be estimated by the empirical averages of the values of F on independent and identically distributed samples {X_i}. A sampling rule called the "screened" estimator is introduced, and its performance is studied. When the mean E(U(X)) of a different function U is known, the estimates are "screened," in that we only consider those which correspond to times when the empirical average of the {U(X_i)} is sufficiently close to its known mean. As long as U dominates F appropriately, the screened estimates admit exponential error bounds, even when F(X) is heavy-tailed. The main results are several nonasymptotic, explicit exponential bounds for the screened estimates. A geometric interpretation, in the spirit of Sanov's theorem, is given for the fact that the screened estimates always admit exponential error bounds, even if the standard estimates do not. And when they do, the screened estimates' error probability has a significantly better exponent. This implies that screening can be interpreted as a variance reduction technique. Our main mathematical tools come from large deviations techniques. The results are illustrated by a detailed simulation example.
@unpublished{konmey07a,
Author = {I. Kontoyiannis and S. P. Meyn},
Note = {{To appear, Annals Appl. Prob.}},
Title = {Computable Exponential Bounds for Screened Estimation and Simulation},
Year = {2006}}
