ODE methods for skip-free Markov chain stability with applications to MCMC
G. Fort, E. Moulines, S. Meyn and P. Priouret
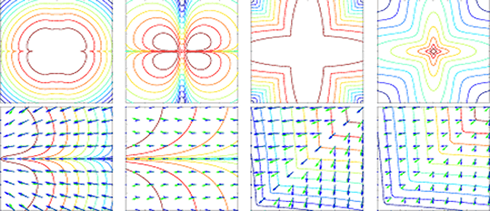 |
The ODE is described as a gradient flow. Shown on the left are contour plots of four target densities, and the corresponding vector field | |
| Shown on the right are sample paths from MCMC in blue, compared with solutions to the associated ODE in red | 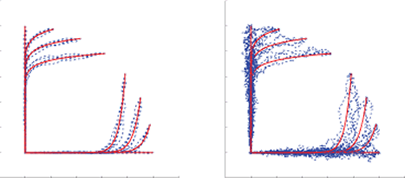 |
Abstract:
Fluid limit techniques have become a central tool to analyze queueing networks over the last decade, with applications to performance analysis, simulation, and optimization. In this paper some of these techniques are extended to a general class of skip-free Markov chains. As in the case of queueing models, a fluid approximation is obtained by scaling time, space, and the initial condition by a large constant. The resulting fluid limit is the solution of an ordinary differential equation (ODE) in “most” of the state space. Stability and finer ergodic properties for the stochastic model then follow from stability of the set of fluid limits. Moreover, similar to the queueing context where fluid models are routinely used to design control policies, the structure of the limiting ODE in this general setting provides an understanding of the dynamics of the Markov chain. These results are illustrated through application to Markov Chain Monte Carlo.
References
@inproceedings{formeymoupri06a,
Address = {New York, NY, USA},
Author = {Fort, G. and Moulines, E. and Meyn, S. and Priouret, P.},
Booktitle = {{Valuetools} '06: Proceedings of the 1st international conference on Performance evaluation methodolgies and tools},
Pages = {42},
Publisher = {ACM Press},
Title = {{ODE} methods for {Markov} chain stability with applications to {MCMC}},
Year = {2006}}
@article{formeymoupri08a,
Author = {Fort, G. and Meyn, S. and Moulines, E. and Priouret, P.},
Journal = ANNAP,
Number = {2},
Pages = {664-707},
Title = {{ODE} methods for skip-free {Markov} chain stability with applications to {MCMC}},
Volume = {18},
Year = {2008}}
See also
@article{bormey00a,
Author = {Borkar, V. S. and Meyn, S. P.},
Journal = SICON,
Number = {2},
Pages = {447--469},
Title = {The {ODE} method for convergence of stochastic approximation and reinforcement learning},
Volume = {38},
Year = {2000}}
