Q-learning and Pontryagin's Minimum Principle

Prashant Mehta and Sean Meyn

Q-learning is a technique used to compute an optimal policy for a controlled Markov chain based on observations of the system controlled using a non-optimal policy. It has proven to be effective for models with finite state and action space. This paper establishes connections between Q-learning and nonlinear control of continuous-time models with general state space and general action space. The main contributions are summarized as follows:

    1. The starting point is the observation that the "Q-function" appearing in Q-learning algorithms is an extension of the Hamiltonian that appears in the Minimum Principle. Based on this observation we introduce the steepest descent Q-learning algorithm to obtain the optimal approximation of the Hamiltonian within a prescribed function class.
    2. A transformation of the optimality equations is performed based on the adjoint of a resolvent operator. This is used to construct a consistent algorithm based on stochastic approximation that requires only causal filtering of observations.
    3. Several examples are presented to illustrate the application of these techniques, including application to distributed control of multi-agent systems.

     

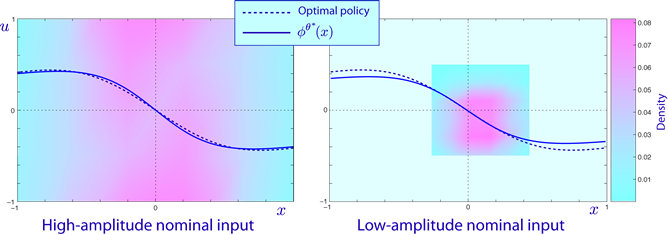
Quadratic cost

Comparison of the optimal policy and the policy obtained from the SDQ(g) algorithm for a scalar example. The approximation is more accurate in the plot shown on the left because the amplitude of the input is larger. The areas in purple indicate state-input pairs that have higher density with the given input signal.

 

 

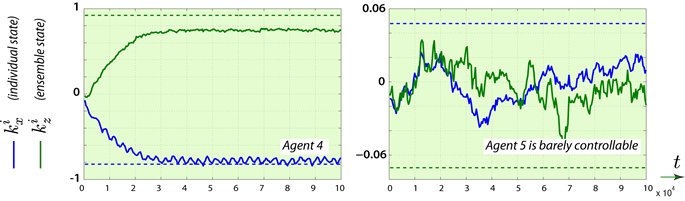
VIA convergence

Sample paths of estimates of optimal parameters using the SDQ(g) algorithm for a multi-agent model introduced in Huang et. al. 2007. The dashed lines show the asymptotically optimal values obtained in this prior work.

Recent presentation on Q-Learning (pdf)

Recent presentation on Quasi-Stochastic Approximation (pdf)

References

@inproceedings{mehmey09a,
Author = {Mehta, P. G. and Meyn, S. P.},
Booktitle = {Proceedings of the 48th IEEE Conference on Decision and Control. Held jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009.},
Month = {Dec.},
Pages = {3598-3605},
Title = {Q-learning and {Pontryagin's} Minimum Principle},
Year = {2009}}

See also Chapter 11 of CTCN, and
@inproceedings{melmeyrib08,
Author = {Melo, F. S. and Meyn, S. and Ribeiro, M. Isabel},
Booktitle = {Proceedings of {ICML} },
Ee = {http://doi.acm.org/10.1145/1390156.1390240},
Pages = {664-671},
Title = {An analysis of reinforcement learning with function approximation},
Year = {2008}}

@inproceedings{shimey11,
Author = {D. Shirodkar and S. Meyn},
Booktitle = {American Control Conference, 2011. ACC '11.},
Month = {June},
Title = {Quasi Stochastic Approximation},
Year = {2011}}

 

spm