Most likely paths to error when estimating the mean of a reflected random walk

Ken Duffy and Sean Meyn

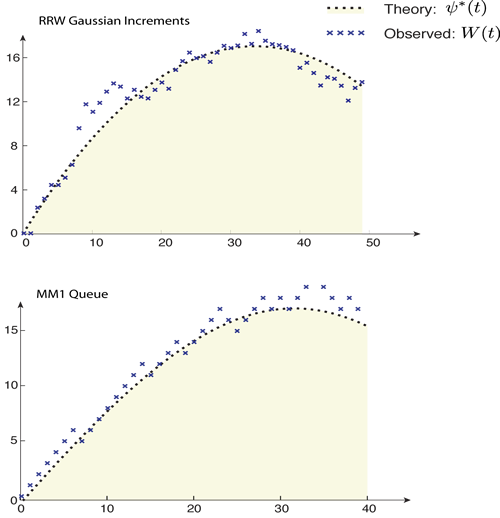
Abstract: Simulation of the mean position of a skip-free Markov chain can be hard, even when the chain is geometrically ergodic. The Large Deviation Principle (LDP) holds for deviations below the mean, but for deviations at the usual speed above the mean the rate function is null. For example, even the stable MM1 queue does not satisfy the LDP. Moreover, this simple model and other reflected random walks exhibit exotic yet quantifiable sample path behavior conditioned on a large sample mean. Two techniques can be used to combat these dynamics to improve simulation algorithms: Multiple control variates, or screening.

Keywords: Reflected random walks, mean position simulation, large deviations, most likely paths.

Fig. 8. On the left are two sets of experiments illustrating the results of the paper. The figure shown on the top shows experiments obtained with Gaussian increments. On the top are results obtained for the M/M/1 queue model in which the increments take on values +/-1. In each case, the observed path has the largest simulated mean out of 100 million sampled paths. Also, shown in each figure is the corresponding theoretical prediction of the most likely path, given the observed simulated mean

The lecture below was presented at the Workshop on Markov chains and MCMC, in honor of Persi Diaconis & Simulation of Stochastic Networks (including RESIM 2010). The Newton Institute, Cambridge University, June 21-23, 2010

Why are stochastic networks so hard to simulate?

View more presentations from Sean Meyn.

References

@article{dufmey10,
Title = {Most likely paths to error when estimating the mean of a reflected random walk},
Author = {K. R. Duffy and S. P. Meyn},
Journal = PE,
Number = {12},
Pages = {1290-1303},
Volume = {67},
Year = {2010}}

@unpublished{blaglymey12,
Title = {Large Deviations for the Empirical Mean of an {M/M/1} Queue},
Author = {J. Blanchet and P. Glynn and S. Meyn},
Note = {{T}o appear in {\it Queueing Systems}, Special Issue on Simulation of Networks},
Year = {2012}}

@article{mey06a,
Title = {Large deviation asymptotics and control variates for simulating large functions},
Author = {Meyn, S. P.},
Journal = ANNAP,
Number = {1},
Pages = {310-339},
Volume = {16},
Year = {2006}}

@book{CTCN,
Title = {Control Techniques for Complex Networks}, %Chapter 11
Address = {Cambridge},
Author = {Meyn, S. P.},
Mrnumber = {MR2372453},
Pages = {xx+562},
Publisher = {Cambridge University Press},
Year = {2007}}