Approximate Dynamic Programming using Fluid and Diffusion Approximations with Applications to Power Management
Wei Chen, Dayu Huang, Ankur Kulkarni, Jayakrishnan Unnikrishnan, Quanyan Zhu, Prashant Mehta, Sean Meyn, and Adam Wierman
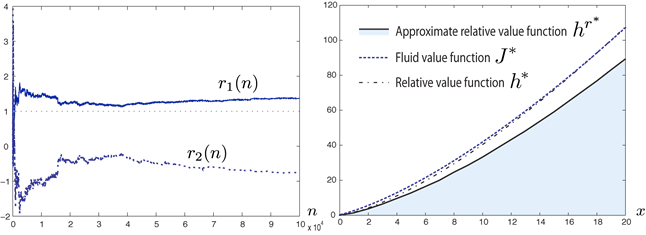
Simulation results for the dynamic speed scale model with quadratic cost. The plot on the left shows estimates of the coefficients in the optimal approximation of the relative value function using the basis obtained from the fluid and diffusion models. In the plot on the right the final approximation is compared to the fluid value function and the relative value function.
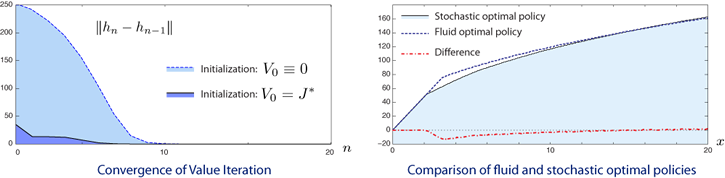
The plot on the left shows convergence of value iteration. The error converges to zero much faster when the algorithm is initialized using the fluid value function. The plot on the right compares the optimal policies for the fluid and stochastic models.
Abstract: TD learning and its refinements are powerful tools for approximating the solution to dynamic programming problems. However, the techniques provide the approximate solution only within a prescribed finite-dimensional function class. Thus, the question that always arises is how should the function class be chosen? The goal of this paper is to propose an approach for TD learning based on choosing the function class using the solutions to associated fluid and diffusion approximations. In order to illustrate this new approach, the paper focuses on an application to dynamic speed scaling for power management.
References
@inproceedings{chehuakulunnzhumehmeywie09,
Author = {Chen, Wei and Huang, Dayu and Kulkarni, Ankur A. and Unnikrishnan, Jayakrishnan and Zhu, Quanyan and Mehta, Prashant and Meyn, Sean and Wierman, Adam},
Booktitle = {Decision and Control, 2009 held jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009. Proceedings of the 48th IEEE Conference on},
Month = {Dec.},
Pages = {3575-3580},
Title = {Approximate dynamic programming using fluid and diffusion approximations with applications to power management},
Year = {2009}}
See also Chapter 11 of CTCN, and
@unpublished{mehmey09a,
Author = {Mehta, P. and Meyn, S.},
Month = {December 16-18},
Note = {48th f Conference on Decision and Control},
Title = {{Q}-Learning and {Pontryagin's Minimum Principle}},
Year = {2009}}
@unpublished{meycheone10,
Title = {Optimal Cross-layer Wireless Control Policies using {TD}-Learning},
Abstract = {We present an on-line crosslayer control technique to characterize and approximate optimal policies for wireless networks. Our approach combines network utility maximization and adaptive modulation over an infinite discrete-time horizon using a class of performance measures we call time smoothed utility functions. We model the system as an average-cost Markov decision problem. Model approximations are used to find suitable basis functions for application of least squares TD-learning techniques. The approach yields network control policies that learn the underlying characteristics of the random wireless channel and that approximately optimize network performance.},
Author = {Sean Meyn and Wei Chen and Daniel O'Neill},
Keywords = {adaptive modulation, radio networks, adaptive modulation, complex interfering networks, cross-layer design, TD learning, network utility maximization, wireless networks},
Note = {Proceedings {IEEE Conference Dec. and Control} (submitted)},
Year = {2010}}
@inproceedings{shimey11,
Author = {D. Shirodkar and S. Meyn},
Booktitle = {American Control Conference, 2011. ACC '11.},
Month = {June},
Title = {Quasi Stochastic Approximation},
Year = {2011}}
