Optimization of Dynamic Matching ModelsAna Bušić and Sean Meyn |
|
|
We consider a discrete-time bipartite matching model with random arrivals of units of supply and demand that can wait in queues located at the nodes in the network. A control policy determines which are matched at each time. The focus is on the infinite-horizon average-cost optimal control problem.
A relaxation of the stochastic control problem is proposed, which is found to be a special case of an inventory model, as treated in the classical theory of Clark and Scarf. The optimal policy for the relaxation admits a closed-form expression. Based on the policy for this relaxation, a new matching policy is proposed. For a parameterized family of models in which the network load approaches capacity, this policy is shown to be approximately optimal, with bounded regret, even though the average cost grows without bound. @article{busmey14,
author = {A.~Bu\v{s}i\'{c} and S. Meyn},
title = {{Optimization of Dynamic Matching Models}},
journal = {ArXiv e-prints},
volume = {abs/1411.1044},Month = {Nov.},
year = {2014}}
|
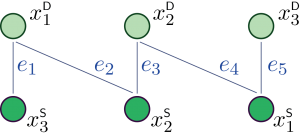
In the simple example shown above there are three classes of demand and three classes of supply. The edges in the graph indicate potential matches.
The paper concerns general bipartite matching models in a stochastic and dynamic setting
|
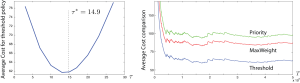
| On the right is the threshold policy for various values of of the threshold tau. The optimal threshold is very close to the value predicted by the RBM model. The plots on the right hand side compare the average cost obtained using the threshold policy (using the diffusion heuristic), MaxWeight, and a priority policy |