Synchronization of Coupled Oscillators is a Game

Huibing Yin, Prashant G. Mehta, Sean P. Meyn and Uday V. Shanbhag

Abstract: The purpose of this paper is to understand phase transition in noncooperative dynamic games with a large number of agents. Applications are found in neuroscience, biology, economics, as well as traditional engineering applications. The focus of analysis is a variation of the large population LQG model of Huang et. al. 2007 [huacaimal07], comprised here of a controlled nonlinear N-dimensional stochastic differential equation model, coupled only through a nonlinear cost function. The states are interpreted as the phase angle for a collection of non-homogeneous oscillators, and in this way the model may be regarded as an extension of the classical coupled oscillator model of Kuramoto.

A deterministic PDE model is proposed, which is shown to approximate the stochastic system as the population size approaches infinity. Key to the analysis of the PDE model is the existence of a particular Nash equilibrium in which the agents `opt out' of the game, setting their controls to zero, resulting in the `incoherence' equilibrium. Methods from dynamical systems theory are used in a bifurcation analysis, based on a linearization of the PDE model about the incoherence equilibrium. A critical value of the control cost parameter is identified: Above this value, the oscillators are incoherent; and below this value (when control is sufficiently cheap) the oscillators synchronize. These conclusions are illustrated with results from numerical experiments.

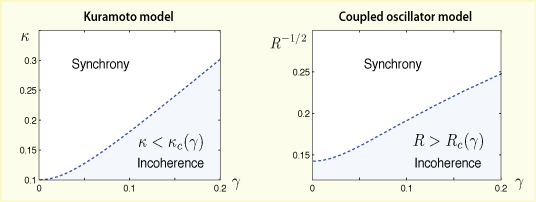		Oscillators synchronize if the coupling is sufficiently large. In the former incoherent setting, the oscillators rotate close to their own natural frequency and hence the individual trajectories are approximately independent of the population. In the synchronized setting each oscillator rotates with a common frequency.

@inproceedings{yinmehmeysha10b,
Author = {Huibing Yin and Prashant G. Mehta and Sean P. Meyn and Uday V. Shanbhag},
Booktitle = {IEEE Conference on Dec. and Control (to appear).},
Month = {December},
Title = {Learning in Mean-Field Oscillator Games},
Year = {2010}}

@inproceedings{yinmehmeysha10,
Author = {Huibing Yin and Prashant G. Mehta and Sean P. Meyn and Uday V. Shanbhag},
Booktitle = {American Control Conference, 2010. ACC '10.},
Note={Submitted for publication, IEEE Trans. Auto. Control},Month = {June},
Title = {Synchronization of Coupled Oscillators is a Game},
Year = {2010}}

@article{huacaimal07,
Author = {Huang, M. and Caines, P. E. and Malhame, R. P.},
Journal = TAC,
Number = {9},
Pages = {1560--1571},
Title = {Large-Population Cost-Coupled {LQG} Problems With Nonuniform Agents: Individual-Mass Behavior and Decentralized {{$\varepsilon$}-Nash} Equilibria},
Volume = {52},
Year = {2007}}