Controlled Lyapunov Functions, Stochastic Model Predictive Control, and Stochastic Dynamic Programming
Below are two papers with a common goal: Apply stochastic Lyapunov concepts from MCSS combined with insights from idealized models to approximate policies for MDPs, or improve convergence in value iteration or policy iteration algorithms.
In more recent work these ideas have formed a foundation for approximate dynamic programming and reinforcement learning architectures:
- Stability and asymptotic optimality of generalized MaxWeight policies
- Q-learning and Pontryagin's Minimum Principle
- Approximate Dynamic Programming using Fluid and Diffusion Approximations with Applications to Power Management
- Optimal Cross-layer Wireless Control Policies using TD-Learning
- Shannon meets Bellman: Feature based Markovian models for detection and optimization
Value iteration and optimization of multiclass queueing networks
R-R Chen and S Meyn
This paper considers in parallel the scheduling problem for multiclass queueing networks, and optimization of Markov decision processes. It is shown that the value iteration algorithm may perform poorly when the algorithm is not initialized properly. The most typical case where the initial value function is taken to be zero may be a particularly bad choice. In contrast, if the value iteration algorithm is initialized with a stochastic Lyapunov function, then the following hold:
- A stochastic Lyapunov function exists for each intermediate policy, and hence each policy is c-regular (a strong stability condition)
- Intermediate costs converge to the optimal cost
- Any limiting policy is average cost optimal
It is argued that a natural choice for the initial value function is the value function for the associated deterministic control problem based upon a fluid model, or the approximate solution to Poisson’s equation obtained from the LP of Kumar and Meyn. Numerical studies show that either choice may lead to fast convergence to an optimal policy.
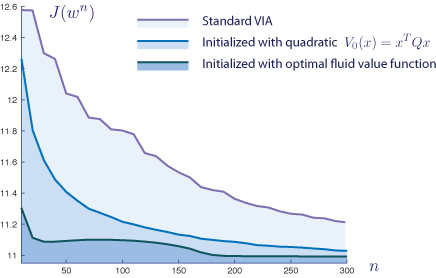 |
Numerical results for a stochastic network: Intialization of value iteration using a quadratic controlled Lyapunov function, or the solution to a deterministic optimal control problem. | |
@article{chemey99a,
Author = {Chen, R-R. and Meyn, S. P.},
Journal = QS,
Number = {1-3},
Pages = {65--97},
Title = {Value iteration and optimization of multiclass queueing networks},
Volume = {32},
Year = {1999}}
The policy iteration algorithm for average reward Markov decision processes with general state space
S Meyn
The average cost optimal control problem is addressed for Markov decision processes with unbounded cost. It is found that the policy iteration algorithm generates a sequence of policies which are c-regular (a strong stability condition), where c is the cost function under consideration. This result only requires the existence of an initial c-regular policy and an irreducibility condition on the state space. Furthermore, under these conditions the sequence of relative value functions generated by the algorithm is bounded from below and nearly decreasing, from which it follows that the algorithm is always convergent. Under further conditions, it is shown that the algorithm does compute a solution to the optimality equations and hence an optimal average cost policy. These results provide elementary criteria for the existence of optimal policies for Markov decision processes with unbounded cost and recover known results for the standard linear-quadratic-Gaussian problem. When these results are specialized to specific applications they reveal new structure for optimal policies. In particular, in the control of multiclass queueing networks, it is found that there is a close connection between optimization of the network and optimal control of a far simpler fluid network model.
@article{mey97b,
Author = {Meyn, S. P.},
Journal = TAC,
Number = {12},
Pages = {1663--1680},
Title = {The policy iteration algorithm for average reward {M}arkov decision processes with general state space},
Volume = {42},
Year = {1997}}
