Phase Transitions and Metastability in Markovian and Molecular Systems
W. Huisinga, S. Meyn, and C. Schuette
See also A Simulation-Based Method for Aggregating Markov Chains (Kun Deng wins the IEEE Best Paper Award), and other references below.
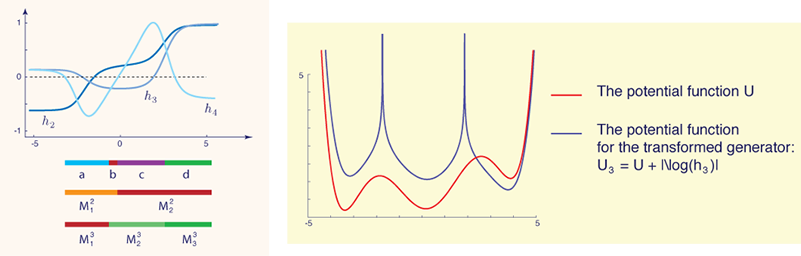
On the left is shown the metastable sets and the shattered state space obtained from the first two eigenfunctions. At right is the potential function that defines the gradient flow in this example, as well as the potential funciton for an associated transformed diffusion.
Abstract Diffusion models arising in analysis of large biochemical models and other complex systems are typically far too complex for exact solution, or even meaningful simulation. The purpose of this paper is to develop foundations for model reduction, and new modeling techniques for diffusion models.
These foundations are all based upon recent spectral theory of Markov processes. The main assumption imposed is V-uniform ergodicity of the process. This is equivalent to any common formulation of exponential ergodicity, and is known to be far weaker than the Donsker-Varadahn conditions in large deviations theory. Under this assumption it is shown that the associated semigroup admits a spectral gap in a weighted L_\infty-norm, and real eigenfunctions provide a decomposition of the state space into `almost'-absorbing subsets. It is shown that the process mixes rapidly in each of these subsets prior to exiting, and that the conditional distributions of exit times are approximately exponential.
These results represent a significant expansion of the classical Wentzell-Freidlin theory. In particular, the results require no special structure beyond geometric ergodicity; reversibility is not assumed; and meaningful conclusions can be drawn even for models with significant variability.
See 2010 survey and prior presentation with review of finite rank Markov models
Reference:
@article{huimeysch04a,
Title = {Phase transitions and metastability in {M}arkovian and molecular systems},
Author = {Huisinga, W. and Meyn, S. and Sch{\"u}tte, C.},
Journal = ANNAP,
Number = {1},
Pages = {419--458},
Volume = {14},
Year = {2004}}
@incollection{schhuimey03,
Address = {Dordrecht},
Author = {Sch{\"u}tte, C. and Huisinga, W. and Meyn, S.},
Booktitle = {2002 IUTAM Symposium on Nonlinear Stochastic Dynamics},
Pages = {71--81},
Publisher = {Kluwer Acad. Publ.},
Series = {Solid Mech. Appl.},
Title = {Metastability of diffusion processes},
Volume = {110},
Year = {2003}}
@article{meyhagmatban08,
Author = {Meyn, Sean and Hagen, Gregory and Mathew, George and Banasuk, Andrzej},
Journal = {Decision and Control, 2008. CDC 2008. 47th IEEE Conference on},
Month = {Dec.},
Pages = {3835-3839},
Title = {On complex spectra and metastability of {Markov} models},
Year = {2008}}
@misc{konmey09a,
Author = {I. Kontoyiannis and S. P. Meyn},
Howpublished = {http://arxiv.org/abs/0906.0259, and submitted for publication.},
Month = {June},
Title = {Approximating a Diffusion by a {Hidden Markov Model}},
Year = {2009}}
@unpublished{denmehmey09,
Author = {Deng, Kun and Mehta, Prashant G. and Meyn, Sean},
Month = {December 16-18},
Note = {{48th IEEE Conference on Decision and Control}},
Title = {A Simulation-Based Method for Aggregating {Markov} Chains},
Year = {2009}}
@inproceedings{densunmehmey09,
Author = {Kun Deng and Yu Sun and Mehta, P.G. and Meyn, S.P.},
Booktitle = {American Control Conference, 2009. ACC '09.},
Month = {June},
Pages = {731-736},
Title = {An information-theoretic framework to aggregate a {Markov} chain},
Year = {2009}}
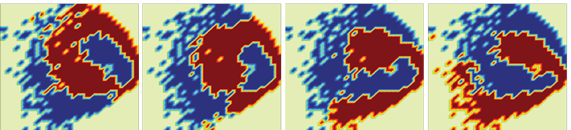 |
A complex eigenvalue near the imaginary axis (cts time) corresponds to a quasi-periodic orbit | |
